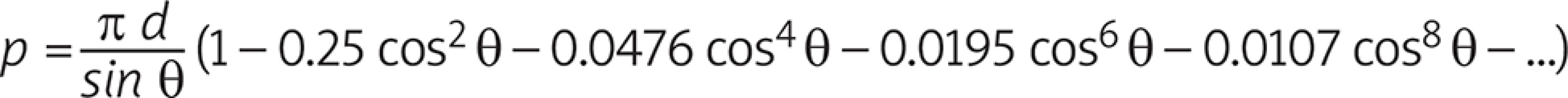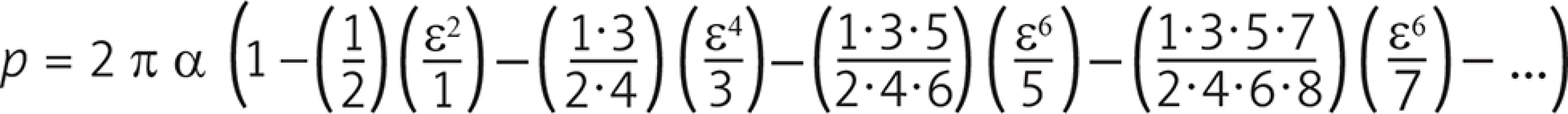Background and rationale of the mathematical model
Maintenance of the he patency of a coronary graft is crucial to improve the long-term prognosis of patients undergoing coronary artery bypass grafting (CABG). Early closure due to the thrombosis of the graft is affected by the perioperative pro-thrombotic effect, which can be amplified by technical factors that reduce graft flow, including anastomotic stricture or hemodynamic factors related to composition of the anastomosis causing slowing of the flow [1–6].
We have studied a mathematical model that has allowed us to evaluate the hemodynamic effects of the flow at the anastomosis point of the coronary artery in relation to the inclination angle of the anastomosis and to the alignment between the main vessel and the inserted vessel, i.e., the saphenous vein graft.
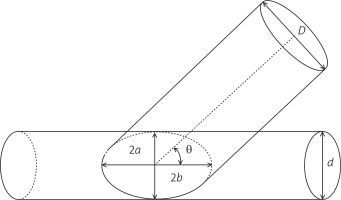
In this research we took two cylindrical tubes of diameter d = 1.5 mm and D = 2.1 mm with a connection as shown in Figure 1 A. A constant flow Q = 0.01 l/min was produced from the diameter tube d, generating a mean velocity of U = 10 cm/s, and the same flow coming from the distal end of the diameter D tube. The two ducts met with an angle θ to which values of 15°, 30°, and 45° were assigned. The results showed the distributions of the velocities (Fig. 1 B), of the pressures (Fig. 1 C), and of the stresses on the wall (Fig. 1 D).
Fig. 1
A – Sketch of the set-up with the main geometrical and flow parameters. B – Color contours of the velocity magnitude in the symmetry plane of the flow for three different angles: θ = 15° (left), θ = 30° (centre) and θ = 45° (right). Contour levels range from U = 1 cm/s (blue) (reference value) to U = 16 cm/s (red). C – The same as Figure 1 B, but for pressure values. Contour levels range from 1 mm Hg (blue) (reference value) to 3 mm Hg (red). D – Shear stress values on the wall. Contour levels range from τ = 1 N/m2 (blue) (reference value) to τ = 6 N/m2 (red)
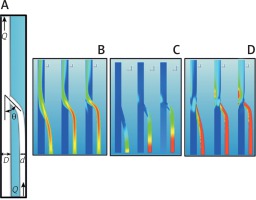
When the angle θ decreased, the input stream tended to align with the direction of the main duct and thus reduced the flow disturbances. If, therefore, no other factors are involved, the duct insertion, i.e. the anastomosis, should be made at the smallest possible angle.
The geometrical setup is that sketched above in which a circular vessel of diameter D has to be joined to another vessel of diameter d < D. Since the circumferential length of the first has to be preserved, the contact line is deformed into an ellipse. In order to maximize the section of the anastomosis, it will result for the ellipse axes 2b = d and 2a sinq = d, θ being the insertion angle of the anastomosis (Fig. 2).
Fig. 2
Mathematical model representation of an anastomosis between the coronary artery (Tube d) and the graft (Tube D), i.e., of autologous saphenous vein
The length of the contact line therefore decreases to the perimeter of an ellipse of semi-axes a and b which would require the integration of a complete elliptic integral of the second kind. Nevertheless, if e = √ [1 – (b/a)2] = cosq is the eccentricity of the ellipse, the integral can be expanded into an infinite series of terms according to:
Upon noticing that a = 2/(2 sinθ) and e = cosθ the above series become the following mathematical model:
It is worth mentioning that the terms drop rapidly to zero since the coefficients keep decreasing and the increasing powers of cosθ make this decrease even faster; as a consequence, retaining terms beyond the fifth does not alter the relevant figures of p.
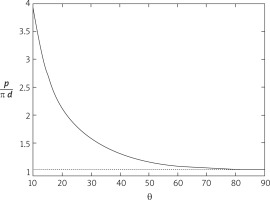
The above formula is plotted on the side figure as a function of the angle θ and it can be noted that as θ decreases the length of the perimeter of the ellipse increases (and for θ → 0, p → ∞).
The determination of the “optimum” angle, therefore, comes from the two opposite needs of minimizing the flow disturbances produced by the anastomosis (which would require θ → 0°) while maintaining the length of p as short as possible (which implies θ → 90°). From the plot of the figure it has been found that the angle θ = 30o allows p to be maintained within a reasonable value (≅ 1.5pd), while limiting the flow disturbances (Fig. 3).
Discussion
The CABG surgery is still widely practiced today. In our center about 250 CABG procedures are performed annually from a total of 500–600 cardiac surgery procedures done, both as isolated and combined, and the care of the technical aspects for the success of an excellent coronary anastomosis is important for the patient’s prognosis.
In the proposed mathematic model, taking as reference the perimeter p* = pd of the diameter of the tube d, the value of the perimeter “p” of the graft anastomosis calculated in centimeters, is p = 1.216 p* for θ = 45°, p = 1.548 p* for θ = 30°, p = 2.709 p* for θ = 15°, respectively. Consequently, taking as a reference the largest diameter of an elliptical circumference, the diameter d of the graft incision obtained with Potts scissors required to make the anastomosis should be about the half of the perimeter value.
As can be seen, the length of p grows very rapidly at the decrease of θ when the latter drops below 30°, which suggests taking this value as a good angle to make the coronary artery anastomosis. The 30-degree value of θ may be optimal for coronary anastomosis, as below this value the perimeter required for anastomosis increases considerably. For example, for a θ angle of 15°, the perimeter of the anastomosis almost doubles, from 1.548p* to 2.709p*. However, based on the results obtained in the mathematical model, at angle θ ranging from 25° to 35°, presumably the graft anastomosis would perform equally well.
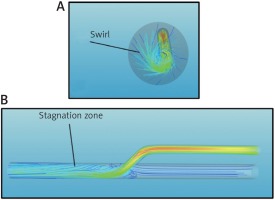
In addition to the inclination of the angle between the two vessels, a further parameter that can cause disturbance in the flow is the misalignment between the main vessel and the inserted vessel. In other words, if the axes of the two ducts are not coplanar, the flow in the anastomosis zone is not in an axial direction but with an angle α that determines a swirl. In this study the simulations were performed for angles α = 10° and α = 20°, respectively. As it is easy to guess, the greater the dissipation between the two ducts is, more intense will be the swirl motion, which generates higher shear stress on the wall of the coronary vessel and a greater loss of pressure in the anastomosis area (Fig. 4 A). Therefore, the incision performed on the coronary vessel should be done perfectly on the axis with the graft, whether the coronary artery bypass is carried out in extracorporeal circulation and cardiac arrest, or on beating heart [7]. In addition to these aforementioned negative effects, the presence of swirl motion is also an indicator of the presence of recirculation areas that are particularly damaging as they potentially cause stagnation of the blood (Fig. 4 B) and, consequently, early thrombosis of the graft [8–12].
Fig. 4
A – Axial view of the stream traces colored by velocity magnitude for an anastomosis performed at an angle θ = 20°. B – The same as Figure 4 A, but for a side view
In conclusion, in the case of coronary surgical revascularization, to reduce the hemodynamic stress on the coronary artery, from the data examined in the mathematical model studied, it appears that an inclination of the anastomotic angle of at least 30° seems to be a right choice when performing a coronary bypass. Moreover, it is necessary to make sure that coronary artery incision is done perfectly correctly in the axis on the graft anastomosis.