Introduction
The ability of magnetic resonance imaging (MRI) to quantify molecular diffusion provides insight into microscopic features of materials and biological tissues at a scale much finer than the image resolution. Diffusion MRI has become a standard tool to grade ischemic lesions and tumors in the brain [1–3] and its applications to study diseases of other organs are gaining ground [4]. A particularly powerful feature of diffusion MRI is the sensitivity to directional properties (anisotropy) of the medium, which opens ways to visualize axonal tracts in the brain [5] and the structure of myocytes in muscles [6] (Table I). Diffusion sensitization is achieved by combining MRI pulse sequences with strong motion-encoding gradient pulses, which cause signal attenuation in the presence of random Brownian motion of water molecules. At the same time, diffusion-sensitizing gradients lead to signal phase shifts in the case of coherent motion of all spins included in an image voxel. This effect constitutes a major challenge for diffusion MRI of moving organs (Table II).
Table I
Diffusion-weighted imaging (DWI)/diffusion tensor imaging (DTI) of the heart – an important research target: Why?
|
Table II
Fundamental challenges in diffusion-weighted imaging of the heart
Diffusion-weighted imaging (DWI) of a heart is particularly challenging due to the scale of the cardiac motion and blood flow, which surpasses the diffusional displacements by a few orders of magnitude and has an enormous impact on the signal phase, up to the effect of complete signal cancellation. Blood flow may cause diffusion coefficient overestimation, while respiration and cardiac pulsation additionally make it difficult to register a signal coming from the heart (Table II). Hence, different approaches have been developed over the years to improve DWI of the heart and enable its quantitative analysis. Immediately after the introduction of the diffusion tensor imaging (DTI) concept for the characterization of anisotropic media, attempts were made to apply it to the heart. However, despite the achievement of many milestones, DTI of the heart in vivo remains challenging. This paper aims to review the major methodological steps taken towards accurate DWI and DTI of the human heart in vivo.
The first DWI of the human heart in vivo
The first attempt at the DWI of a human heart in vivo was performed by Edelman et al. [7] in 1994. The main advantage of applying DWI seen by the authors was the possibility to obtain structural information about the myocardium, such as fiber orientation or compartmentalization. They proposed to address the difficulty of a bulk heart movement by the first application of an echo planar imaging (EPI) method that is synchronized with the cardiac cycle (Table III). At the same time, they applied a stimulated spin echo (STE) pulse sequence with a breath hold.
Table III
Milestone advances in DWI/DTI of the heart
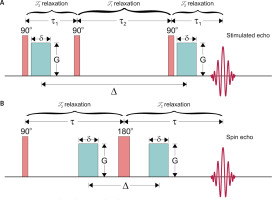
Breath holding prevents the respiratory movement influencing diffusion measurements. STE relies on the application of three 90° radiofrequency (RF) pulses. The first two are separated by a diffusion-sensitizing magnetic field gradient (or dephasing gradient) and the second one is followed by the diffusion time. After that, the third RF pulse and subsequently the second gradient (or rephasing gradient) are applied and the diffusion-weighted signal (echo) is encoded (Figure 1 A). During diffusion time magnetization is stored along the main magnetic field, B0, which makes it sensitive to T1 rather than T2 relaxation (see Figure 1 for comparison of spin echo and stimulated echo pulse sequences). This enables a longer interval between magnetic field gradients to be used without the total loss of a signal, and long enough to use electrocardiographic (ECG) gating.
Figure 1
Stimulated (STE; A) and spin (SE; B) echo pulse sequences for diffusion encoding with marked dominating relaxation processes in given intervals. 90° and 180° blocks are radiofrequency (RF) pulses that flip magnetization to transversal plane and invert spin phases, respectively, τ1 and τ2 are separation times of the first two and last two 90° RF pulses, τ is 90° and 180° pulses’ separation time, green blocks are diffusion gradient pulses with amplitude G, duration δ and separation Δ. Note: that registered signal,
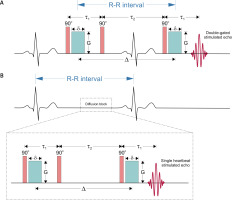
The technique proposed by Edelman et al. relied on two gate triggers set after some time (delay) after two R-waves (called double gating, see Figure 2 A). The diffusion (Δ) and echo times (TE) were equal to the R-R interval and 42 ms, respectively, while gradient duration was 10 ms. The b-value achieved for such time conditions was 395 s mm–2, while for the standard approach with rectangular gradient pulses the b-value is calculated from,
Figure 2
Schematic representation of double-gated stimulated echo (STE) pulse sequence (A) in comparison to single heartbeat STE (B) for diffusion measurement. 90° is the radiofrequency (RF) pulse that flips magnetization to the transversal plane, τ1 and τ2 are separation times of the first two and last two RF pulses, green blocks are diffusion gradient pulses with amplitude G, duration δ and separation Δ, which is a diffusion time considerably smaller than the R-R interval for the single heartbeat encoding (Table III)
where ϒ is gyromagnetic ratio, δ is diffusion gradient pulse duration, G is diffusion gradient amplitude and Δ is two diffusion gradient pulses’ separation time (Figure 1). In order to assure the same cardiac cycle during dephasing and rephasing gradients, trigger delays have to be equal. Spin-echo EPI (SE-EPI) proved to be insufficient for obtaining artifact-free DWI, while only very low b-values (~20 s mm–2) enabled the registration of a signal of a heart.
Development of DTI of the heart in vivo
Desensitization to motion effects in DTI
The first full diffusion tensor in vitro and in vivo with strain measurements
Myocardial function can be associated with the size of chambers, inotropic stimulus, but also the heart muscle fiber architecture. Diffusion anisotropy reflects the local structural orientation of the tissue [8], which led Garrido et al. [9] to determine it in order to obtain fiber architecture of the rat’s myocardium in vitro. Real anisotropy of the tissue required assessment of a full diffusion tensor. Even though this first attempt of DTI was performed on the intact heart, it delivered preliminary information about diffusion anisotropy in the myocardium.
The in vivo implementation of DTI was introduced by Reese et al. in 1995. They adopted the ECG-double-gated STE pulsed field gradient (PFG) technique proposed by Edelman et al. as efficient for motion compensation, in which they recognized another effect of material strain upon the NMR spin physics. To correct for the myocardial deformation at each location across the whole cardiac cycle, they assumed linear phase deformation conjugated with the stretch tensor of a material. The true diffusion tensor could be determined from the apparent one and a strain history obtained independently by NMR methods. Besides the full diffusion description and information about its anisotropy, the proposed method provided a new tool for studying the dynamics of fiber architecture in vivo (Table I). For example, the authors demonstrated that with the application of their methodology it was possible to compare strain rate and wall thickness (represented by the highest eigenvalue) distribution widths, which confirmed the hypothesis of transmural equalization of fiber shortening relative to wall thickening.
Strain-corrected DTI in vivo without strain history measurements
Even though having significant capabilities, the method proposed by Reese et al. [10] for strain correction is complex and time-consuming, leading to reduced SNR and increasing the risk of systematic errors (Table II). Indeed, dilation and contraction can have a relevant influence on diffusion coefficients, but these processes can be omitted if diffusion is encoded in the characteristic moments defined by Tseng et al. and called “sweet spots” [11] (Table III). They developed an approach of finding sweet spots by relying on a very important observation that myocardial strains are highly synchronous and can be accurately approximated by the periodic time-dependent scaling of a fixed strain image. If this scaling fulfils certain requirements at a given moment in time, then the measured diffusion tensor is a true one. As the authors pointed out, periodicity and continuity of scaling function confirm the existence of at least two sweet spots, which in a cardiac cycle are located in mid-ejection and in mid-filling. Later, it was shown that the systolic phase has advantages over the diastolic phase, mainly the thicker myocardial wall with smaller requirements for spatial resolution and lower sensitivity to heart-rate variations [12].
Despite the two key approximations made, that diffusion is linearly dependent on strain and that strain history can be obtained without local material tracking as proposed by Reese et al. [10], the associated error for diffusion measurements is less than 6% and 2%, respectively. Sweet point miss-targeting leads to the error rate of 0.4% per millisecond of time shift. The method proved to be effective for obtaining reliable DTI data of a beating heart with acceptable error and provides reproducible fiber orientations (Table III).
Flow-compensated strain correction
Concerned about the possibility of occurrence of various cardiac motions unrecognized in strain measurements or other unanticipated mechanisms that can influence diffusion experiments, Dou et al. presented another method for strain correction [13]. It relies on the application of two bipolar diffusion-sensitizing gradients, while the bipolarity of the second one (after the second R-wave) provides flow compensation. Bipolar diffusion gradients per se produce diffusion sensitization only during their duration, which was reported to be about 30 ms [13]. It is shorter than the myocardium contraction time, which makes the diffusion measurements strain-insensitive. This is contrary to unipolar diffusion gradients, for which diffusion sensitization occurs during the whole cardiac cycle (up to the end of the rephasing, unipolar gradient), which makes the measurements strain-sensitive.
The proposed methodology has the advantage of encoding diffusion only over a single cardiac phase (Figure 2 B). During a bipolar gradient pulse strain effects can result from a residual phase modulation if the gradient lobes are not the same shape, but remain negligible. Due to limitation of the gradient strength for clinical applications, obtaining the desired b-value (300–400 s mm-2 based on previous papers) imposes long diffusion-encoding times. This increases TE and reduces SNR and spatial resolution, which can be improved by the application of stronger magnetic field gradients (Table II).
Introduction of SE-EPI for in vivo cardiac DTI
Single-shot, double-gated EPI, after being proposed by Edelman et al. [7], became a powerful tool for the diffusion measurements of the beating heart (Table III). Its choice was obvious due to the ability of rapid data acquisition for the entire image. In combination with STE, it makes the diffusion measurements almost insensitive to bulk motion. Eventually, by encoding e.g. at the mid systole of the cardiac cycle by using bipolar gradients, it seems that diffusion measurement reflects reasonably (within acceptable error level) the undisturbed diffusion in the myocardium within two heartbeats (diffusion time is equal to R-R interval). However, STE-EPI has a major drawback over the SE pulse sequence of a very low SNR [12] (Table II). Gamper et al. found that SNR in flow-compensated (double bipolar diffusion gradients) SE-EPI can be more than 8-fold higher than in STE [12]. In spite of this fact, they showed some requirements that the diffusion experiment by using SE must fulfil.
Simulations of phase distribution of moving spins within the myocardium revealed significant phase gradients if an inappropriate voxel size is chosen [12]. It was shown that in order to obtain an undistorted image of the myocardium, one has to choose as far as possible some specified voxel size for a given b-value and systole phase. For uncompensated flow in the mid-systole this required resolution is very high (< 0.5 mm2) for b = 200–600 s mm–2 and hard to obtain. Using bipolar rephasing gradient leads, besides flow compensation, to reduction of the required resolution to 4–5 mm2 for the same b-value range.
The other important modification for cardiac diffusion imaging that was proposed by Gamper et al. is the application of the inner volume imaging method reported by Feinberg et al. [14] in the early years of MRI. This method is also called reduced field of view (FOV) and briefly relies on reducing the excitation or acquisition of the volumes smaller than the whole object. This method provides only the volume of interest without the necessity to image the surrounding tissues to avoid artifacts (such as aliasing). The main advantage of reduced FOV is considerable reduction of measurement time, enhanced resolution and improved image quality. Therefore, it allowed Gamper et al. to obtain 5-fold acquisition speedup and achievement of the diffusion image in a single heartbeat. This methodology was later adapted by Deux et al., who used a 75% FOV and a partial k-space acquisition (87.5%) [15]. Such practice aims at reducing the time between the excitation pulse and readout center, which limits the sensitivity of EPI to the magnetic susceptibility differences (Table II).
Navigator-gated DTI
Cardiac MRI can be performed at either end-expiration or end-inspiration. In both of these respiratory phases susceptibility artifacts can be seen (Table II), while their location is shifted towards the apex at the end-inspiration phase [16]. The end-expiration leads to a significant decrease of respiratory motion artifacts [16] and is more pronounced due to the higher reproducibility [17]. For example, in the work of Gamper et al., the authors collected data for over 420 heartbeats during free breathing and chose the most frequent one for the image reconstruction based on an intensity correlation [12]. This image served as a navigator of a myocardium at the expiratory phase. Such an approach for modulus averaging was at that time a new technique for respiratory compensation alternative to breath holding [7] and synchronized breathing [10] proposed at the beginning of cardiac DTI (Table III).
The importance of this navigator-gated imaging of the heart in vivo was noticed by Nielles-Vallespin et al., who performed reproducibility tests of these technique in comparison to the multiple breath-hold approach [18]. Both techniques showed good reproducibility of DTI parameters. Even though navigator-based measurements exhibited longer duration, lower SNR and statistically different helix angle values compared to the breath-holding technique, some of these problems can be eliminated by the development of accept/reject algorithms as stated in the work. As indicated by the authors, development of navigator-based DTI is of great importance for patients with cardiovascular disease and limited breath-holding capacity. In addition, the navigator approach, alongside the single heartbeat SE-EPI, is suitable for arrhythmic patients [17, 18].
Second- and higher-order motion compensation
Diffusion-prepared steady-state free precession
DTI techniques encoding diffusion during a single heartbeat like those presented by Gamper et al. [12] and Nielles-Vallespin et al. [19] are highly desirable, especially for clinical patients, since they allow free breathing (Table III). However, they bear a major obstacle for the achievement of the b-value appropriate to reach restrictions in the myocardium (~350 s mm-2), which is relatively short diffusion time (tenths of the R-R interval) (Table II). This imposes the necessity of application of long diffusion gradients (10 ms for a maximum gradient of 45 mT/m [19], which is an usual maximum gradient strength available clinically), which is undesirable for cardiac applications, or relatively strong gradients not available in clinical practice (87 mT/m for a gradient duration of 8.3 ms [12]).
To address the issue of single heartbeat diffusion encoding by clinically available gradient strengths, Nguyen et al. developed a new diffusion-prepared pulse sequence with second order motion compensation (such as acceleration) based on steady-state free precession [20] (Table III). Briefly, the method consisted in ECG triggering, a navigator and two blocks during the diastolic quiescent phase: diffusion preparation (90° excitation pulse, two 180° refocusing pulses and a 90° tip-up pulse that stores magnetization in the longitudinal direction; four diffusion bipolar pulses that yield second order bulk motion compensation and are applied throughout the entire block, which ends up with the spoiler gradient) and the balanced steady-state free precession sequence to get image information. The advantage of the proposed sequence is the separation of diffusion encoding and the image readout. It reduces the sensitivity of the signal to T2 relaxation, because image gradients do not contribute to TE, and allows the combination of different diffusion-encoding schemes with various image readouts. Moreover, it can be used for three-dimensional imaging. The study confirmed the sequence’s suitability for clinical applications (weak gradients) and delivered artifact-free DW images with reasonable diffusivities in comparison to uncompensated motion sequences, which yielded highly overestimated values. However, there must be considered a trade-off between motion-compensated, single-heartbeat diffusion encoding and slightly reduced SNR due to longer TE = 115 ms (resulting from the diffusion preparation), while the feasibility of clinical cardiac imaging within a single heartbeat seems invaluable.
Comparison between first- and second-order motion compensation DTI
Advanced research in cardiac diffusion MRI allowed the establishment of a methodological consensus concerning the best measurement approach related to SNR, motion compensation and the optimal protocol (ECG triggering, reduced FOV, resolution, etc.) as presented above. Further development was later focused on the improvement of these issues. Having accepted that accurate DTI of the heart relies on the optimized, speeded-up SE-EPI with motion compensation and short TE suitable for T2 relaxation times in the myocardium (Table II), other advanced approaches were developed in addition to the one described in section “Diffusion-prepared steady-state free precession”
Stoeck et al. reported such a method for the first- and second-order motion compensation based on spin echoes [21] (Tables II, III). The design of the diffusion-encoding pulse sequence relied on two bipolar gradient pulses with appropriately fitted lobe duration (while the inverted lobe is adjacent to the first lobe) for the efficient nulling of the desired gradient moment (different for the first- and second-order motion compensation), and separated by a variable rate selective excitation (VERSE) pulse. The high gradient strength used in this study (80 mT/m) delivered b = 450 s mm–2, which is higher than typically used (~300–350 s mm–2). This suggests that the second order flow compensation can also be achieved with slightly lower gradients. However, higher gradients can provide stronger signal attenuation or its registration from tighter spaces and slower species. A significant reduction to TE down to 73 ms was also achieved.
In the study, several interesting observations were made when comparing first- and second-order motion compensation in DTI. First of all, in contrast to the first-order motion-compensated diffusion encoding, mean diffusivity from the second-order motion-compensated diffusion encoding proved to be insensitive to trigger delay. Moreover, it had a smaller standard deviation within the myocardium and across volunteers. Finally, the second-order motion-compensated DTI delivered physiological transmural distributions such as a linear dependency of the helix angles on the transmural depth, while no such dependency was seen with the first-order compensated DTI method. Based on these results it can be seen that the developed method for second-order motion compensation is significantly less sensitive to bulk motion, and is reproducible for different systolic phases and parts of the heart (from base to apex).
Higher-order motion-compensating diffusion gradients
The method proposed by Stoeck et al. for second-order motion compensation diffusion encoding, even though efficient, was tested on a high-performance gradient system [21]. As pointed out by the authors, if weaker gradients were used, they had to be longer. The increased duration of diffusion gradients results in increased sensitivity to the bulk motion deviated from the first- and second-order one. Studies providing deeper insight into the higher-order heart motion can also be found (Table III). Gradient moment nulling has been found to be simple and appropriate for the motion compensation, but for example, for each successive order of motion the number of gradient pulses is doubled, which considerably increases TE for the achievement of a given b-value [22]. It also has drawbacks connected with potential gradient waveform modifications (it works only for fixed timings).
Higher-order motion compensation pulse sequence was proposed by Welsh et al., and relied on specially designed diffusion gradient waveforms (the same waveform duration, but having variable amplitudes) based on bipolar pulses placed on either side of the refocusing RF pulse [22]. The total number of gradient pulses was equal to four for acceleration (second-order) and six for jerk (third-order) compensation. In contrast, jerk-compensated diffusion encoding by gradient moment nulling via binomial expansion [21] (the same gradients’ amplitude) could be provided by a total of ten pulses and would increase the required diffusion time for a given b-value. The proposed method was tested in vivo in rats and proved to be sufficient, since it delivered reliable fractional anisotropy (FA) maps and myofiber orientation. The main drawback is decreased SNR due to longer TE, although it is an inherent element for higher-order motion compensation requiring more gradient pulses (Table II). An indisputable advantage is the fact that the designed gradient pulse sequence can be implemented in STE. In STE attainable b-values can be increased from 350 to 680 s mm–2. Even though the trigger delay window is narrower for SE than for STE, if the trigger delay is carefully selected, both techniques can perform similarly for compensation of motion and eddy currents [23]. Moreover, scan time can also be shortened if parallel imaging techniques are used. Following the authors, the necessary compromise among b-value, SNR and motion compensation can be sufficiently achieved for this approach, which offers an alternative in case of a lack of high-performance gradient hardware.
Prospects for further cardiac DTI improvements
Diffusion has been proposed as a natural biomarker for many diseases, mainly neurodegenerative [24, 25], but also musculoskeletal [26, 27] or cardiovascular [28–30]. Despite their potential, DWI and DTI indices are not used routinely in clinical practice as biomarkers of cardiovascular diseases, since they require sophisticated experimental methods as presented above. However, it was recently shown that based on standard SE-EPI, DTI is feasible for patients with acute myocardial infarction (AMI) (Table I), when sequence parameters are carefully chosen on the basis of a pilot DTI [29]. Figure 3 presents images from DTI examination of a patient with AMI, shortly after pPCI (5 days), applying the same sequence design. The results showed a very good agreement with late gadolinium enhancement images, including infarction damage zones as well as microvascular obstruction. This proves that DTI has potential to be commonly used in clinical practice for AMI patients as an alternative to gadolinium contrast agent (Table I). Hopefully, this and similar applications will be used routinely and pave the way for more advanced methods to enable accurate quantitative DTI and diffusion to become a natural biomarker of cardiovascular diseases. Although progress in cardiac DTI is clearly visible, more solutions are sought to bridge the gap between the scientific development and clinical practice.
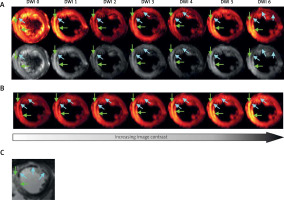
Figure 3
Images from patient with AMI (5 days after pPCI) obtained by using SE-EPI DTI sequence with details given previously [29]. A, B – and T1-weighted imaging with late gadolinium enhancement. A – Raw DWI images for b = 0 s mm–2 (DWI 0) and for six non-collinear diffusion gradient directions (DWI 1-6) required for diffusion tensor calculation: hot scale (upper row) and grey scale (bottom row); B – method for visualization of damage zones with different severity by using increasing image contrast; C – T1-weighted image with late gadolinium enhancement. Green arrows indicate infarction area – hyperintense spots in comparison to remote tissues, while blue arrows indicate microvascular obstruction – signal loss
During the cardiac DWI and DTI development many milestones have been reached, including motion compensation, achievement of the optimal b-value and resolution, choice of the most appropriate cardiac phase, desensitization to T2 relaxation and SNR improvement. All of them helped to approach accurate quantitative DWI and DTI, which in the latest papers have delivered generally reproducible values of ADCs and DTI parameters for the myocardium. It is expected that further steps will be taken to move from more common STE to SE-based DTI [31] to improve SNR without the necessity for image averaging, which may lead to erroneous diffusion tensor indices (Table II).
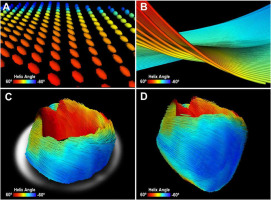
Another advance has been sought in diffusion tensor tractography of the myocardium. Exemplary myocardium tractography is shown in Figure 4, which was adapted from Lee et al. [32] and reflects three-dimensional mouse heart muscle fibers. Myocardium tractography is especially challenging in comparison to other tissues, such as nervous tissue, due to the lack of long structures in a heart muscle. Instead, it is made of syncytia of microscale cardiomyocytes. This results in the problem of the adjustment of a tract fiber length threshold, which often serves as a tool for the elimination of mistracked fibers or short tracts. The latter might appear when eigenvectors and eigenvalues have been misdetermined due to systematic errors, which leads to tracking algorithm fail. The second threshold that is important for high quality tractography is associated with anisotropy measures, such as fractional anisotropy (FA) [33]. However, the values of FA differ strongly among papers, even for healthy controls. We hypothesize that some of these differences may derive from systematic errors resulting from an inhomogeneous magnetic gradient field [34].
Figure 4
Unmodified Figure 4 from: Three-dimensional cardiomyocytes structure revealed by diffusion tensor imaging and its validation using a tissue-clearing technique; “Representative image of mouse heart DTI. A – Zoomed-in view of 3D diffusion tensors calculated at each voxel in the short-axis plane. Orientation of the anisotropy of the diffusion tensor is conventionally assumed to be parallel to the underlying cardiomyocytes orientation. Diffusion tensors are color-coded based on the calculated helix angle. B – Zoomed-in view of 3D cardiomyocytes tracking in the myocardium. C – Reconstructed cardiomyocytes above the mid-left ventricle on a short-axis plane. D – 3D tractography of the helix angle of a mouse heart visualizes the helical structure of the cardiomyocytes twisting around the left ventricle.” By Lee et al. [32] licensed under CC BY 4.0 [34]
The recently developed b-matrix spatial distribution (BSD) calibration method aims at the elimination of systematic errors influencing the calculation of a diffusion tensor [35–37]. It was shown that on the grounds of the generalized Stejskal-Tanner equation [38] it is possible to accurately determine b-matrix, which leads to improved DTI indices and tractography [35, 37]. Moreover, the BSD approach is more straightforward in comparison to the alternative methods relying on the so-called coil tensor, L, obtained from the manufacturer or experimentally [39]. The method or an approach based on its simplified form has been successfully applied for living tissues, such as the brain [40, 41], skeletal muscles [27], and recently also in the myocardium [29]. In the myocardium, a noticeable improvement was observed for the FA value [29]. We believe that the BSD method can be applied for the enhancement of DTI in the myocardium as in other anisotropic media.
Conclusions
DWI/DTI of the human heart has been an important research target with potential clinical applications. Over the years, new developments have emerged with respect to increasing the accuracy and diagnostic value of DWI/DTI of the human heart in vivo. A number of applications of DTI in vivo and ex vivo have been suggested for the characterization of myocardial structure, fiber architecture, dynamics and diseases. Progress in cardiac DTI allowed the establishment of the most suitable cardiac phase, motion compensation and diffusion weighting. Even though further developments are required in terms of TE shortening, acquisition time reduction, higher-order motion compensation or improved SNR, cardiac DTI is clinically feasible. This exciting research area has promising clinical relevance considering that it can deliver microstructural information and reflect the physiological status of a muscle non-invasively. Thus, DWI/DTI cardiac imaging may provide a deeper insight into macroscopic cardiac functions, empowering clinical diagnosis.








