Purpose
Certainly, Monte Carlo (MC) simulation is the most accurate approach of dose computation showing many advantages [1]. For instance, brachytherapy source photon beams can be modelled accurately, and characteristics of photon and electron transports in a heterogeneous media can consider [1]. Accurate modelling of brachytherapy source requires full details of the geometry information and components’ compositions. This is because, if there are errors in the geometry information and components’ compositions, increased uncertainties of dose calculation can occur. Therefore, these details are usually provided by manufacturers.
Recently, many works in brachytherapy have studied dose distributions around radioactive sources. Monte Carlo codes, including MCNPX [2], PENELOPE [3], Geant4 [4, 5], and EGSnrc [6], are specifically built to simulate charged particles transport and radiation interaction, with matter at energy levels used in medical physics [7].
Geant4 Code [8] originally designed for high energy physics experiments has been used in many applications, such as nuclear physics and space sciences. While allowing simulation of low energy particles, its applications are also extended to medical physics. This study comprised Geant4 code MC-based dosimetry in accordance with AAPM TG-43UI [9] protocol for flexi high-dose-rate (HDR) 60Co source (Elekta AB, Stockholm, Sweden) [10] and microSelectron HDR 192Ir (Nucletron, The Netherlands) [2]. The goal of this study was to compare the various dosimetric parameters of TG-43UI [9] of the two sources in a water phantom. In the literature, some authors have published relevant dosimetry data with different methodology for both the sources. Vijande et al. [10] reported a dosimetric characterization of flexi 60Co source using Geant4 [4, 5] and PENELOPE [3]. Recently, Almansa et al. [5] published a complete dosimetric characterization of Elekta flexi 60Co HDR source using PENELOPE Monte Carlo code. Moreover, Williamson and Li [11] and Kirov et al. [12] published an extensive base of dosimetry data based on MC calculations, thermoluminescent dosimeter (TLD), and diode measurements, including dose-rate constants and anisotropy functions for the microSelectron HDR 192Ir radionuclide source. Similarly, Russel and Ahnesjö [13] performed MC calculations based on EGS4 code of the same quantities in a water phantom, and considering electron binding energy of scattering atom in incoherent scattering process. Karaiskos et al. [14] also calculated dose-rate distribution in a water around this source using analytical MC simulation. Furthermore, Zabihzadeh et al. [2] calculated TG-43 parameters based on MCNPX Monte Carlo code.
In this study, the Geant4 [15] Monte Carlo code was used to calculate the TG-43 dosimetric parameters, with the same methodology for the two sources. Dose rates were determined considering the photon transport only. Anisotropy functions F(r, θ) and radial dose g(r) were compared with other published data for the sources and between each other, whereas dose-rate constants were compared with the published data only. To the best of our knowledge, no research has been published comparing TG-43 parameters of both microSelectron 192Ir and flexi 60Co HDR radionuclide sources using Geant4 Monte Carlo simulation.
Material and methods
Source description
MicroSelectron HDR 192Ir source (model No., 105.002) consists of a 3.50 mm long active source, with a diameter of 0.60 mm enclosed in a 0.85 mm diameter 304 stainless steel capsule (density of 7.8 g/cc). The tip of encapsulation is assumed to be a 0.108 mm thick conical section, with a half angle of 23.6° and radius of the face of 0.17 mm. The conical section is attached to a 0.49 mm long solid cylindrical section, followed by a 3.6 mm long hollow section with an inner diameter of 0.335 mm. Following the hollow section of a 0.40 mm long solid conical section with a half-angle of the cone is assumed to be 24° attached to the conical section of a 0.5 mm section of 304 stainless steel cable. The reason to consider only a 5 mm long cable and not a longer one was based on the specifics of clinical setting. In clinical applications, where the portion of a cable near the source is aligned with the axis of a source, doses around the cable are, in general, insignificant. Consequently, the cable length considered in the simulations is not a crucial issue [8, 16]. Figure 1A shows the geometry of microSelectron HDR 192Ir source used in MC simulation.
Fig. 1
A schematic drawing illustrating the structure of: A) HDR microSelectron 192Ir source [2] and B) HDR flexi 60Co source [10]
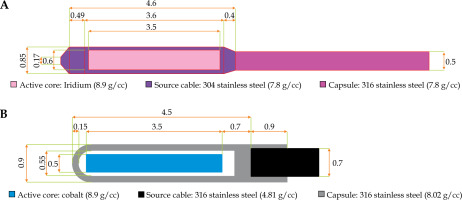
The source design, dimensions, and materials of flexi 60Co HDR source was provided by the manufacturer, and shown schematically in Figure 1B. It is composed of a central cylindrical active core made of metallic 60Co, with a density of 8.9 g/cc, 3.5 mm in length and 0.5 mm in diameter [10, 14, 17]. The active core of flexisource 60Co radionuclide source is covered by a cylindrical 316L stainless steel of elemental composition by weight (67% Fe, 11% Ni, 18% Cr, 2% Si, 2% Mn) [5, 10], with density of 8.02 g/cc. For this study, 2 mm length and a 0.7 mm diameter 316L steel cable was included, with a mass density of 4.81 g/cc. Interstitial areas for 60Co source between the active element and the cover were surrounded by an air shell of 0.05 mm thick, and air shell was encapsulated by a layer of 0.9 mm of external diameter stainless steel [2, 5]. These dimensions were applied to re-create a model of the source in Geant4.
Monte Carlo calculations
Monte Carlo methods are statistical simulation methods that provide approximate solutions to a wide variety of physical and mathematical problems by performing statistical sampling processes, which utilize a sequence of random numbers and probability to obtain an approximation to the problem under simulation. For this work, the geometry and tracking (Geant4 toolkit) [15] version 11.0 was applied for the simulation study. Geant4 is an object-oriented MC toolkit written in C++ language for simulating the passage of particles through matter [18]. It covers a broad range of functionalities, including complex geometry definition, physical processes modeling, particle tracking, and hits recording. This toolkit has been applied extensively to MC simulation related to brachytherapy [18]. The accuracy of Geant4 simulation methods for external radiotherapy and internal brachytherapy have been previously established [8, 19].
Geant4 defines particle type and physics processes in physics list class [20]. We used low energy package of Geant4 in the physics list class for modeling of Compton scattering, photo-electric effect, and Rayleigh scattering processes [21]. Class library in Geant4 provides several random number engines. In our application, the RanecuEngine was chosen at the beginning of the main program [18]. It was then possible to reset random number seed between runs in our program. General particle source method was applied to define a primary source particle. In this method, many internal commands for definition of the source position, geometry, and type of emitted particle were defined in the G4General-ParticleSource class. These commands were done through a macro file without any change in the main program.
We considered the 60Co flexisource used in this study composed of two gamma energies: 1.173 MeV and 1.332 MeV as well as the radiation spectrum of microSelectron of 192Ir source obtained from the National Nuclear Data Center database [20]. The β spectrums of both of simulated sources were neglected because it did not contribute to dose-rate distribution due to encapsulation within the stainless steel [8, 21]. Dosimetric characterization of brachytherapy sources has been one of the medical physics applications of the code [5, 16, 22]. TG-43 formalism calculated the dose rate distributions around brachytherapy sources according to the following equation [6, 9, 18]:
where Sk is air-kerma strength of brachytherapy source, which can be specified in terms of air-kerma rate, at a point along the transverse axis of the source in free space [6, 9]. It is defined as the product of air-kerma rate (Kair (d)) at a calibration distance, d in free space, measured along the transverse bisector of the source and the square of the distance (d) [6, 23].
where θo = 90°; the air-kerma rate (K.air), in Gy/s of source activity (A) in Becquerel and the number of photons per decay (Np) was determined from:
The air-kerma strength per unit source activity was then calculated as:
Or
where U = µGym2 h–1 = cGycm2 h–1.
The dose-rate constant in water (Λ) is the ratio of the dose rate at the reference distance (ro = 1 cm, θo = 90°) on the transverse axis per a unit air-kerma strength, and its unit is cGyU–1h–1.
The dose-rate constant depends on both the radionuclide and source model, and is influenced by both the source internal design and the experimental methodology used by the primary standard to realize SK.
G(r, θ) is the geometry function, which accounts for the effect of the distribution of radioactive material inside the source on the dose distribution at a given point according to:
where L is the active length of the source, β is the angle subtended by the active source with respect to the point (r, θ), and G(r0, θ0) is the geometric function at reference point (r0 = 1 cm and θ0 = 90°).
The radial dose function g(r) accounts for dose fall-off on the transverse plane due to photon scattering and attenuation:
The anisotropy function F(r, θ) represents the variation of the dose distribution around a brachytherapy source due to the distribution of radioactivity within the source, self-absorption, and oblique filtration of the radiation in the capsule material, which defines as:
From different parameters of TG-43 equations Sk, Λ, and G(r, θ) refer to the source specification and its geometrical shape according to the manufacture design.
To estimate the dose-rate constant, the radial dose function g(r) and the anisotropy function F(r, θ) of the sources were located in the center of a 2 × 2 × 2 m3 cube of a phantom. The dose-rate constant in water (Λ) was the ratio of the dose-rate at the reference distance on the transverse axis per unit of air-kerma strength. The air-kerma strength was calculated along the transverse axis of the source in the air-filled cubic phantom using mesh scoring with a voxel size of 2 × 2 × 2 mm3. The air composition recommended in table XIV of the TG-43 update [9] for air was applied, with a relative humidity of 40%. Deposited doses in air and water were calculated around the source using the PrimitiveScore class and mesh scoring method. PrimitiveScore is an abstract base class representing a detector for dose scoring in Geant4. The dimension of each voxel in mesh scoring was set to be 2 × 2 × 2 mm3. The deposited doses in air and water in these voxels were then converted to the TG-43 calculated parameters, such as Λ, g(r) and F(r, θ) using equations (6), (8), and (9), respectively.
Uncertainty analysis
In this study, uncertainties associated with MC process were considered according to the AAPM task group report No. 138 and GEC-ESTRO recommendations [18, 24]. The type A (∇Λ) uncertainty for MC methods was due to the numbers of events, where Poisson statistics applies; this uncertainty decreases by the inverse square root of the number of particles. The number of photons simulated was set to 109 to achieve an uncertainty of less than 0.1%. Type B uncertainties arise from uncertainties in the source dimensions, internal component location, volume averaging, and material composition. This affects the MC simulation, more specifically, the dose-rate constant, radial dose, and anisotropic functions for a specific simulated brachytherapy source. Uncertainties associated with the dose-rate constant ∇Λ, radial dose ∇g(r), and anisotropy functions ∇F(r, θ) for both 60Co and 192Ir sources were considered according to a comparison of our results from the MC simulation with values of the AAPM task group report No. 138 and GEC-ESTRO reports [24]. Finally, the total dose uncertainty was calculated through the following equation:
Where
Results
The results of calculations of the-dose rate constant for HDR microSelectron 192Ir and HDR flexi 60Co sources obtained from the simulations by Geant4 code in the 2 × 2 × 2 m3 cube of water phantom with a voxel size of 2 × 2 × 2 mm3 are presented in Table 1. The dose-rate constant was used to specify the radioactive sources and depended on both the radionuclide and source model. The percentage dose-rate constant difference for 60Co and 192Ir between the MC result and the published report was 0.2% and 1.1%, respectively.
Table 1
Dose-rate constant values (cGyh–1U–1) for HDR microSelectron 192Ir and HDR flexi 60Co source in a water phantom
| Present study | Other studies | Diff. (%) | |
|---|---|---|---|
| 60Co | 1.089 | 1.087 [25, 26] | 0.2 |
| 192Ir | 1.097 | 1.108 [27] | 1.1 |
Figure 2A and B shows a comparison of the radial dose function between our MC results and published data for 192Ir and 60Co, respectively [26, 28], with percentage differences of 1.1% for 192Ir and 1% for 60Co (Table 2). Figure 2C and D also demonstrates a comparison between the anisotropy dose function at 1 cm radial distance between our MC results and published data for 192Ir and 60Co, respectively [26, 28], with percentage differences of 1.5% for 192Ir and 1.3% for 60Co. In addition, the type A and B uncertainties for both HDR microSelectron 192Ir and HDR flexi 60Co sources obtained from a comparison between the MC calculated values are indicated in Table 2. The total uncertainty of MC simulation for the HDR flexi 60Co source was 1.7% and that of HDR microSelectron 192Ir was 2.2%. The error intervals in each case were in accordance with the AAPM TG No. 138 [24].
Fig. 2
A comparison between our MC results and published data at 1 cm depth. A) Radial dose function of HDR flexi 60Co, B) radial dose function of HDR microSelectron 192Ir, C) 2D anisotropy function of HDR flexi 60Co, and D) 2D anisotropy function of HDR microSelectron 192Ir
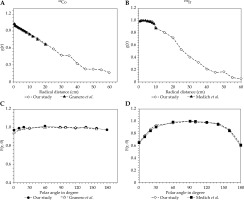
Table 2
Percentage dose difference obtained from a comparison between MC calculated values and published data [26, 28] as well as uncertainties of 192Ir and 60Co sources determined from MC simulation
Figure 3A compares the radial dose functions for the two sources from 0.5 cm to 60 cm radial distances. Radial dose function associated with 192Ir was higher than that of 60Co at radial distances from 3 to 20 cm, with the maximum percentage difference of 8.1% observed at 5 cm distance, whereas it was lower at larger distances from the source. The radial dose function of HDR flexi 60Co source was linearly fall-off from 1 cm to 20 cm of radial distances, whereas for 192Ir it was from 5 cm to 20 cm.
Fig. 3
A comparison between MC results of HDR flexi 60Co and microSelectron 192Ir. A) Radial dose function, B) 2D anisotropy function at 1 cm, C) 2D anisotropy function at 3 cm, and D) 2D anisotropy function at 4 cm
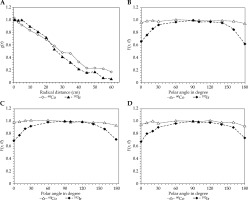
Compared with the values of HDR microSelectron 192Ir source, anisotropic dose distributions of HDR flexi 60Co source were significantly higher at the longitudinal sides of the source. The anisotropy functions for the two sources at radial distances of 1 cm, 2 cm, and 4 cm are compared in Figure 3B-D.
The primary photons from the HDR flexi 60Co source had a greater range, and were attenuated at a lower level when considering the results of radial and anisotropic dose distribution functions, whereas the primary photons from the lower energy HDR microSelectron 192Ir source had a smaller range and were partially attenuated. This means that compared with a 192Ir source, 60Co radionuclide could be utilized to treat malignancies farther away from the source, even though the 60Co radionuclide source has a larger exit dose than iridium.
Discussion
In this study, the dosimetric comparison between the microSelectron HDR 192Ir and the flexi 60Co sources was evaluated in a liquid water phantom, and the calculations were performed with Geant4 Monte Carlo simulations. As a result, the dose-rate constants were verified based on MC simulation of the BEBIG 60Co HDR source [25, 26] for the flexi 60Co HDR source and flexisource HDR 192Ir source [27] for the microSelectron 192Ir source. The percentage difference between the dose-rate constant value from this study and the published data was 0.2% and 1.1% respectively, as indicated in Table 1. Papagiannis et al. [6] deduced the dose-rate constants for point source of 60Co HDR, and reported an uncertainty value of 0.2%. In another study, Ranjbar et al. [18] have shown also approximated 0.2% percentage difference between the calculated and published date. Zabihzadeh and Arefian [2] in their work on tumor dose enhancement by nano-particles during high-dose-rate 192Ir brachytherapy reported the uncertainty value between the calculated and published values as 1.06%.
The dose fall-off on the transverse plane caused by photon attenuation and scattering in the water medium is accounted for by the radial dose function g(r). Additionally, the anisotropy function F(r, θ) and the geometry factor G(r, θ) have an impact. The geometry component is influenced by the source’s physical characteristics, such as its length and radius. The sources’ construction must be identical to ensure the same geometry factors. In clinical dose distribution, the isodose curve is influenced by the anisotropy factor F(r, θ). These two functions are necessary for comparing various brachytherapy sources [6]. Results of the radial dose function and the anisotropy dose functions for both sources were verified at 1 cm depth using BEBIG 60Co HDR [26] and HDR 192Ir [28] sources, respectively. As demonstrated in Table 2, the percentage dose difference of each function with the corresponding published data was below 2%, in an acceptable range according to the recommendation of AAPM TG43-U1 [9] and TG 138 [24].
Figure 3A compares the radial dose functions, and at 5 cm depth, the microSelectron 192Ir source recorded 8.1% higher dose than the flexi 60Co source. The values of the radial dose function of 60Co are lower than those of 192Ir within the range of 3 cm to 20 cm radial distances and linearly fall-off from 1 cm to 20 cm distances, but are higher from 0.5 cm to 1 cm and above 20 cm. From 5 cm to 20 cm, the value of the 192Ir radial decline linearly. Employing the EGSnrc Monte Carlo transport algorithm, Islam et al. [29] evaluated the radial dose distribution for the BEBIG HDR 60Co and microSelectron HDR 192Ir v. 2 sources. They found that the 60Co source had greater values in the region of 0.18 cm to 1 cm and above 22 cm of radial distance compared with the 192Ir source.
In comparison with microSelectron 192Ir source HDR values, the anisotropic dose distributions of the flexi 60Co HDR source are significantly higher at the longitudinal sides of the source. The primary difference may result from the sources’ varied geometric constructions, source types, choice of angle interval, and average energy differences [6, 16, 30].
Conclusions
Both 60Co and 192Ir isotopes have a long history in the field of brachytherapy. Several hundred HDR afterloading units equipped with 60Co or 192Ir sources have been put into use in the past. The average energy of a brachytherapy source determines the penetrability of photon particles emitted from the source. High energy sources allow a higher dose to target at larger distances to the sources. Therefore, the primary photons from the lower-energy HDR microSelectron 192Ir source have a limited range, and are partially attenuated when considering the results of radial and anisotropic dose distribution functions. This implies that a HDR flexi 60Co radionuclide could be used to treat tumors farther from the source than a 192Ir source despite the fact that HDR microSelectron 192Ir has a lower exit dose than HDR flexi 60Co radionuclide source. Hence, the treatment planning system should adjust the isodose distribution using dwell time positioning technology in a clinically relevant manner.


