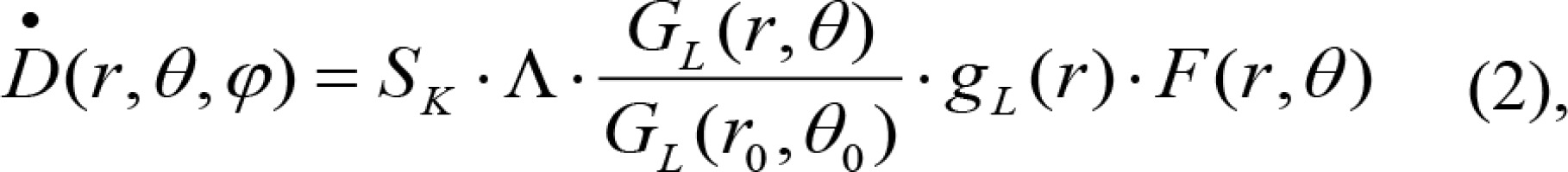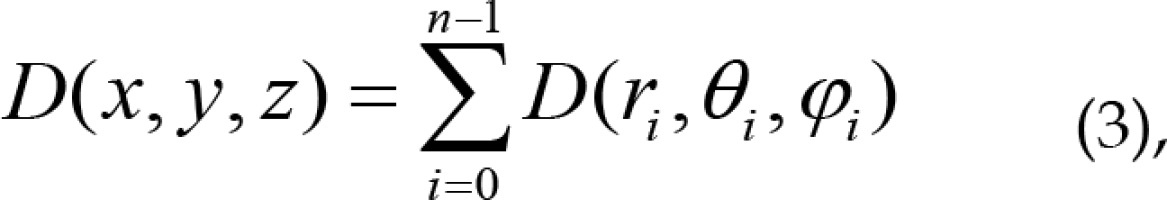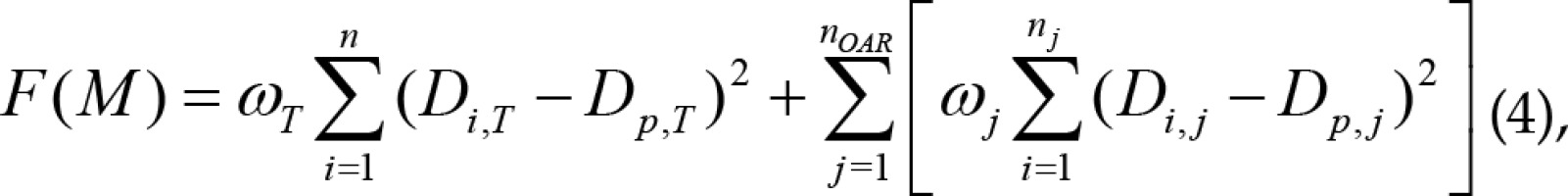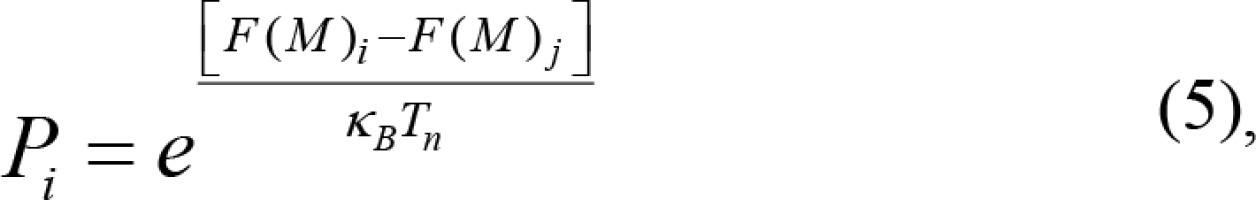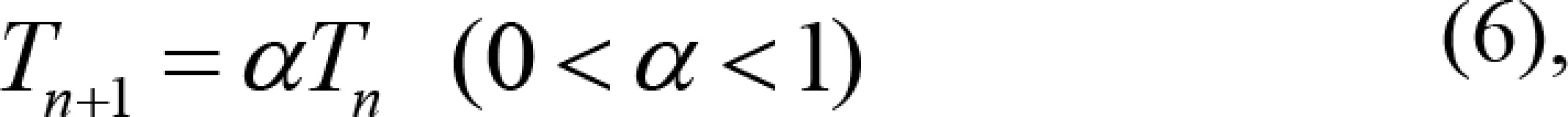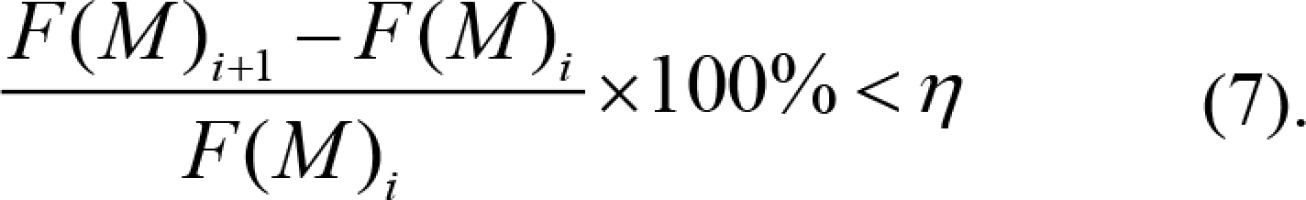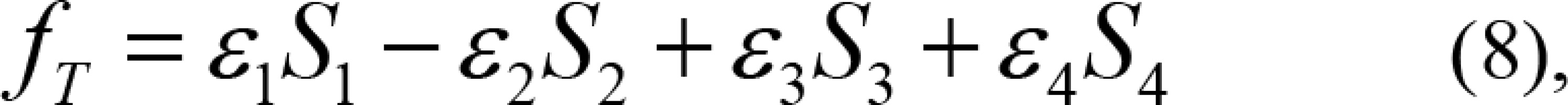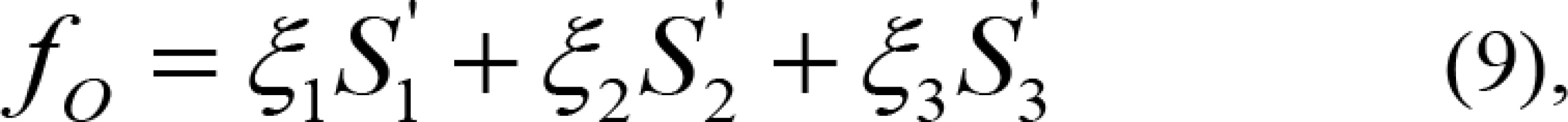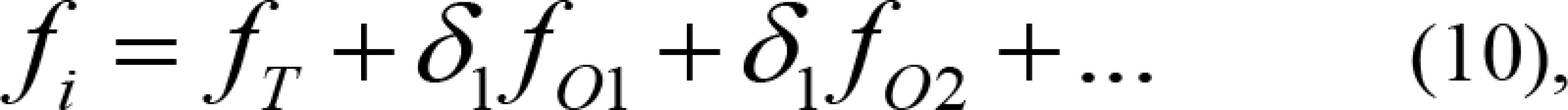Purpose
Malignant cancer is the leading cause of death in both men and women in the world [1]. By implanting Iodine-125 (125I) seeds into the target, the radioactive dose can be adapted to the shape of target volume. Since the dose intensity is inversely proportional to the square of the distance [2], the dose accumulated in normal tissues around the target is minimized. A number of studies on 125I seeds implantation for prostate cancer has achieved acceptable results [3,4,5,6]. Thus, 125I seeds implantation, with its satisfactory effectiveness, has been accepted as one of the methods of prostate cancer treatment.
With regards to 125I seeds implantation surgery, the preoperative dose planning is the key to successful operation. Dose planning in high-dose-rate brachytherapy is developing rapidly and at the moment, there are many well-known inverse optimization procedures [7,8,9]. However, the inverse optimization method is rarely applied to 125I seed brachytherapy (low-dose-rate brachytherapy), and dose planning is mostly completed manually by the physician.
In recent years, a number of researches on 125I seed brachytherapy based on the coplanar template have been published [10,11,12]. While, in clinical practice, a typical coplanar template is designed with parallel needle guiding holes, evenly arranged at 5 mm interval in a 13 by 13 matrix or a 17 by 17 matrix. Therefore, the needle puncture path is uniquely fixed. Considering dose distribution to the target, it is inevitable that occasionally the puncture path can be blocked by bones or other critical tissues, when the template is used in brachytherapy. In addition, the fixed path leaves a narrow space between the needle and other critical tissues or organs, which increases the risk of injury during the procedure. Some researches show that multiple independent templates can intensify flexibility in patient specific treatment planning and receive better treatment planning results [13]. Currently, there is no commercial treatment planning system available, which allows non-coplanar needle insertion and automatic treatment plans. Therefore, a novel method for an arrangement of needle with adequate dose distribution is urgently needed, combining flexible non-coplanar needle with effective dose planning.
In the last two decades, due to the development of computer technology, many optimization methods for dose planning in seed brachytherapy have been proposed [14,15,16]. However, the inverse planning technique is still investigated. Comparing with traditional optimization methods such as the Manchester [17] and Paris systems [18], the inverse treatment planning could achieve a balance between dose distribution and optimization time, with more accurate dose planning. The inverse optimization algorithm is different from the traditional dose planning. Firstly, it needs to set the goal to be achieved. Then, the objective function based on the constraint conditions should be determined. Finally, the iterative search method is used to find the optimal solution.
Dose volume histogram (DVH) curve has a weak connection with the geometries of organs. In numerous studies, the optimization is established by setting a series of constraints on DVH or matching the DVH to referenced ones [19]. Xing et al. established a dose optimization framework for incorporating metabolic information from functional imaging modalities into the intensity-modulated radiation therapy with inverse planning process [20]. Cotrutz’s group proposed a new inverse planning scheme with voxel-dependent importance factors [21], in which the planning procedure can be divided into two steps. After the completion of a conventional trial-and-error inverse planning procedure, the dose interval is identified to locate the voxels that receive the dose in the selected range. Mountris et al. proposed an inverse planning approach that can improve planning quality by combining DVH without compromising the overall execution times [22]. However, most DVH-based optimization algorithms are mostly used in external radiotherapy, and only a small number of specialists consider the evaluation of DVH with the automatic optimization of seeds distribution.
The aim of this article is to propose a new optimization method based on non-coplanar needle, which combines an inverse optimization algorithm with a DVH evaluation method called ‘the hybrid inverse optimization method’.
Material and methods
Planning procedure
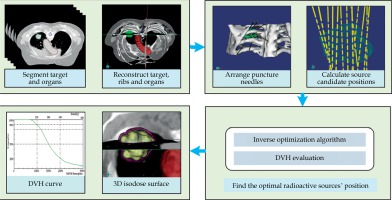
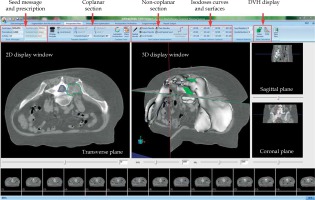
A new tool was proposed to help the physician to acquire the treatment plan. The general workflow is presented in Figure 1.
Firstly, the geometric boundary of the tumor based on manual segmentation and the planning target volume (PTV) was obtained by the physician, and the skeleton based on computerized tomography (CT) value was automatically extracted. Secondly, the puncture needles were assigned and adjusted manually by the physician to cover the target. Since the non-coplanar needle was used in this process, there was no need to consider the direction of needle. Thirdly, the hybrid inverse optimization algorithm was applied to search for optimal seed distribution for each seed number (minimum distance between two seeds positions was 5 mm). Finally, the DVH evaluation method was used to determine the optimal seeds distribution.
Non-coplanar needle assignment method
The coplanar template is commonly used to install the puncture needle in ultrasonic-guided brachytherapy of prostate cancer, and achieves good results, since there are no barriers for needle puncturing. The template ensures the exactly perpendicular location of puncture needle, which guarantees high precision and helps physician to perform the intra-procedure rapidly.
Dose distribution is often unable to meet the clinical demand, when using a coplanar template to treat a multifocal metastasis of lung cancer. Given that, the parallel needles in a coplanar template are difficult to cover all areas and dose distribution is not able to reach the prescription dose. To avoid bones and ensure dose coverage when the tumor is vertebra metastasis or in the shade of bones, we developed a dose planning method based on non-coplanar needle, with each needle to be adjusted in any direction.
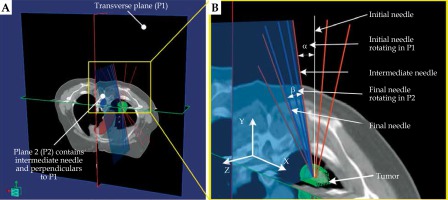
The position adjustment of non-coplanar needle is illustrated in Figure 2. The initial needle was in the transverse plane (P1), parallel to Y-axis. Supposing, the length of the needle is l, its center point is C, and its tip point is T. Firstly, the needle center was placed at C (x, y, z) point. Secondly, the initial needle was rotated around C by α to obtain an intermediate needle. Then, a new plane (defined as P2) perpendicular to P1 was created, containing the intermediate needle. Finally, the intermediate needle was rotated around C by β to attain the final needle in P2.
Fig. 2
A) The adjustment of non-coplanar needle in the three-dimensional space and (B) in partial magnification
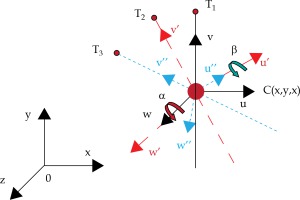
Therefore, the needle center C and the needle tip T were chosen to control the position of the needle. The relative coordinates of needle tip are shown in Figure 3, which are respectively marked as o-xyz, o1-uvw, o2-u′v′w′, and o3-u″v″w″. The transformation process was described as follows. Firstly, the needle was translated along X-axis with x, Y-axis with y, and Z-axis with z to acquire o1-uvw. Secondly, the needle was rotated around the W-axis by α to get o2-u′v′w′. Finally, the needle was rotate around the U′-axis by β to reach o3-u″v″w″. Consequently, the final position of the needle tip T3 can be obtained from the below formula [23]:
Fig. 3
The transition of needle tip’s position. Point C is the center of the needle. T1, T2, and T3 are the position of the needle’s tips. The red dashed line represents the result of the first rotation, and the blue dashed line represents the result of the second rotation
(1)
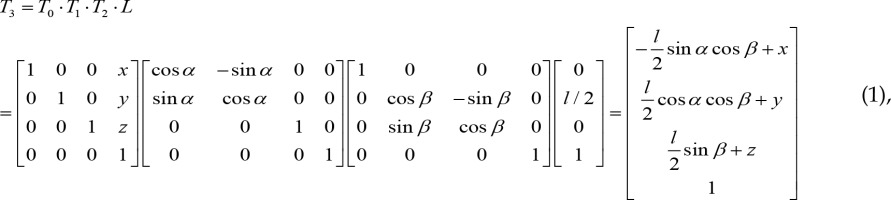
where T0 is the translation matrix of the puncture needle relative to the coordinate system o-xyz. T1 and T2 are the rotation matrices of the puncture needle with respect to the W-axis and U-axis, respectively.
Radiation dose calculation model
The 125I (6711) seed involved in this research was shaped in cylinder, with a length of 4.5 mm and diameter of 0.8 mm. The seed was wrapped with 0.05 mm titanium, and iodide ion adsorbed with radiation activity of 0.7 mCi as internal. The dose rate was calculated using the TG-43 U1 protocol [24] published by AAPM, as shown in equation (2):
where Sk is the air kerma strength of the source, Λ is the dose rate constant, G(r, θ) is geometry factor, gL (r) is radial dose function, and F(r, θ) is anisotropy function. r represents the distance from the center of the active source to the point of interest, r0 denotes the reference distance, which is specified to be 1 cm in the protocol, and θ signifies the polar angle specifying the point-of-interest relative to the source longitudinal axis. θ0 denotes the source transverse plane and is specified to be 90°.
Dose rate calculation model for spatial multiple seeds was based on scalar superposition, which means that the dose rate at a point in space is equal to the sum of the dose rate of all the seeds at that point. Suppose there was a point P(x, y, z) in the dose space, regardless of tissue heterogeneity and inter-seed attenuation, the total dose of n seeds can be calculated as equation (3):
The optimization framework
The purpose of dose planning for conventional brachytherapy is to obtain an ideal dose distribution. On the one hand, there is sufficient radiation dose in the target to terminate the tumor cells. On the other hand, the organs at risk (OARs) are prevented from being damaged by radiation dose. In this research, the hybrid inverse optimization algorithm was proposed to better achieve the purpose, in which an inverse optimization algorithm and a DVH evaluation method were involved. Firstly, the number (denoted by Ne) of seeds needed was calculated based on the Anderson nomogram [25], according to the geometry of the target area and the type of seed. Since the shape of the target was irregular in the actual situation, more seeds were needed to provide sufficient radiation dose. The upper limit of the number of seeds can be set to a large value, but this leads to increased computational time. Moreover, multiple simulations demonstrated that the maximum number of seeds after optimization was 1.3 Ne.
At that time, the hybrid inverse optimization method was carried out to find the optimal seed position. The number of seeds Ns, ranging from Ne to 1.3 Ne, was inputted to run the optimization program and then, each optimal solution was obtained. Finally, DVH evaluation method was included to determine the optimal result.
Objective function of the inverse optimization algorithm
Seed implantation aims to deliver the dose to cover PTV as much as possible. At the same time, organs at risk (OARs) should be irradiated minimally. Therefore, the objective function needs to consider all these factors by setting the weight coefficient of each organ’s objective function. For this purpose, a multiple objective function F with penalty value of each organ was given by equation (4):
where T refers to the target volume, p denotes to the prescription dose, and ω refers to the weighting factor of the target volume or OAR. n refers to the number of interest points in the target, nj refers to the number of interest points in the OAR, and nOAR refers to the number of OARs. In addition, Di refers to the dose of each interest point, and Dp denotes to the prescription dose of the target or the tolerated dose of OAR.
In terms of the contradictory goals that minimize the dose variation, the prescription on the surface of the tumor PTV will also minimize the dose to the OARs. All these factors were involved in equation (4), so that physicians can choose the best prescription dose for the target and the tolerated dose for OARs, according to their clinical experience. Then, the minimal F(M) can be determined through the inverse optimization algorithm. To determine the weighting factor and to avoid large number of trials, a multi-criteria optimization (MCO) was involved [26].
Optimization by the inverse optimization algorithm
The inverse optimization algorithm used in this research is the simulated annealing [27], which is analogous to a crystal seeking its lowest energy, as it slowly decreases from a high initial value. As a kind of stochastic algorithm, it is suitable for an optimal dose allocation. This research improves the determination of the initial value in simulated annealing. In the simulated annealing algorithm, in order to obtain the global optimal solution, a large initial value needs to be established. However, the number of seeds can be determined based on the tumor volume (nomogram), thus it is easy to determine the initial value. In the iteration process of the seed distribution, each layout scheme has an evaluation function and a corresponding constraint condition. The inverse optimization algorithm determines whether to accept a new distribution according to the evaluation function, so that the evaluation function in the distribution model would be expressed as a quantitative index. The evaluation function was in fact the objective function we mentioned before. According to equation (4), F(M) > 0. Furthermore, it is clear that the smaller the value of F(M), the better the current state. According to the Metropolis criterion [28], F(M)i was the evaluation function of the current state of i. Then, a disturbance was made to the state i, and a new state j with its evaluation function F(M)j can be obtained. If the evaluation function F(M)j < F(M)i and j for the optimal condition, the radioactive seeds distribution will jump to state j from state i. If F(M)j ≥ F(M)i, with distribution state of j inferior to the state of i, the transition will be in accordance with a certain probability of Pi, which was called the acceptance probability:
where κB denotes the Boltzmann constant, n is the nth iteration, Tn is the parameter that controls the reduction of the initial value, and α controls the reduction rate of the initial value. That is, the slower the rate, the more accurate the inverse optimization algorithm results, and vice versa.
In this algorithm, there are two ends conditions. The first one was that the initial value Tn decreased to zero through the equation (6). The initial value should be high enough to prevent the algorithm from falling into the trap of a local optimal solution. The second end condition was the equation (7). The algorithm terminated when the change in the result of two adjacent iterations was less than a certain value η. The smaller the value of η, the more accurate the optimization result, but the optimization time will be longer.
The DVH evaluation method
Clinically, DVH contains a number of important indicators that reflect the effect of treatment. DVH describes the cumulative dose received by a certain percentage of tumor volume or organ volume. In DVH, the Y-axis represents the volume (V) and the X-axis represents the dose (D). Vx means the fraction of volume that received x% of the prescription dose, and Dx means the dose received by the fraction x of the volume. The relationship between tumor or organ and dose distribution can be observed from the curve. However, DVH cannot reflect the real geometric information of the tumor or organ. In addition, it cannot reflect the number and distribution of seeds. Hence, we can firstly build a reference DVH model and then, the result of the inverse optimization algorithm can be evaluated by comparing the practical DVH curve with the model.
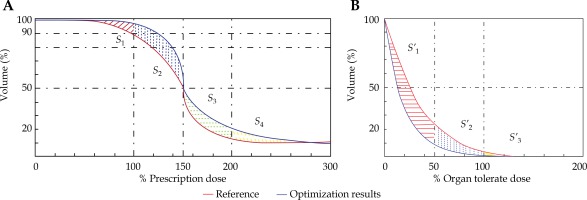
In the seed implantation surgery for thoracoabdominal tumors such as lung and liver, there may be guidelines missing to evaluate the DVH. Dose irradiating a small volume (D0.1cc, D2cc), which may be correlated with the side effects, are generally reported. The dose homogeneity index (DHI) [29] is the target receiving a dose between 100% and 150% of the prescription dose, and that is DHI = (V100 – V150)/V100. To ensure the curative effect of tumor, the dose planning target requires that 90% of target volume receives at least 100% of the prescription dose (V100 ≥ 90%). In addition, V150 < 50% and V200 < 25% were set to avoid the delivery of excessive dose to the patient. In the DVH evaluation model, as shown in Figure 4, the red line represents the reference and the blue line denotes one of the current results of the inverse optimization algorithm. For PTV, V100, V150, and V200 were chosen as the turning point and four areas, V0-V100 (S1), V100-V150 (S2), V150-V200(S3), and V200-V300 (S4) were defined. For the target, the blue DVH was better than the red DVH, as shown in Figure 4A. S1 and S2 were above the reference line, showing that the results were better. The result’s quality is calculated from the size of S1 and S2 areas, where for increasing S1 and decreasing S2 areas, the quality increases. S3 and S4 were below the reference line, showing that the results were better. Similarly, the result’s quality is quantified from the size of S3 and S4 areas, where for increasing S3 and S4 areas, the quality increases. Therefore, we can define the quality of the PTV of current DVH:
Fig. 4
Red line represents reference DVH curve, and blue line denotes the practical DVH curve (the resulting one from the optimization). A) The image on the left shows the target evaluation model; B) The image on the left shows OAR evaluation model
where ε1, ε2, ε3, and ε4 are the weighting factors of each areas.
For OARs, in Figure 4B, S’1, S’2, and S’3 represent the areas where the DVH after optimization was better than the reference DVH, and the larger the area, the better the optimized DVH. The function for evaluating OAR was given as follows:
where ξ1, ξ2, and ξ3 are the weighting factors of each area.
Therefore, the evaluation equation, combining PTV and OARs, can be defined as follows:
where fi is the optimal result of number i seeds in the inverse optimization algorithm (the larger, the better). δ1 and δ2 are the weighting factors of each OAR, which are small numbers.
The reference DVH (based on non-coplanar needle) was obtained from one of the cases screened by physician that met the dose requirements. Comparing with the reference DVH, the physician managed to create a rank of selected DVHs manually, based on clinical experience. Then the best weighting factors of DVH evaluation function were selected to match the manual ranking results. After that, the weighting factors were incorporated into DVH evaluation function. Finally, all the results acquired from the inverse optimization algorithm were compared to evaluate a max fi as the ultimate optimization result. The final results were not influenced if the reference DVH was changed or if another physician was estimating the ranking. Firstly, the reference DVH should meet the requirements of V100 ≥ 90%, V150 < 50%, and V200 < 25%. Secondly, when compared with the reference DVH, the sizes of S1, S2, S3, and S4 should be considered. Therefore, if the reference DVH was changed and if another physician evaluated the ranking, the DVH of the optimal result will not be influenced by the change, but the sizes of S1, S2, S3, and S4 will be different.
Experimental platform construction
In order to implement our new planning method, a brachytherapy treatment planning system (BTPS) was designed using VTK, ITK [30,31], and the Microsoft Visual Studio 2010 software (Figure 5).
Case studies
All the images in the study were CT images (DICOM 3.0) of 5 mm spacing between slices, and the voxel resolution was 0.70 × 0.70 × 5.00 mm3. The first test was designed to examine the performance of the hybrid inverse optimization algorithm and to compare the difference between non-coplanar needles and coplanar needle planning. BTPS was run on a Dell computer with Intel Core i7 3.60 GHz CPU and 8 GB RAM. The second test was carried out to investigate the practical application of the new technique. In order to improve the computing speed of the method, the minimum cube of the wrapped target was extracted firstly and then extended 50 mm in every direction, as the dose optimization area. Additionally, the calculation range of single seed model was set to 50 × 50 × 50 mm3 by balancing the accuracy of dose and the speed of program. Moreover, the non-coplanar needle’s spacing was between 5 mm and 10 mm, and the needles with seeds were placed with 5 mm intervals. Furthermore, the optimization time was also recorded and included: finding the number of seeds based on nomogram (Ne), repeating the optimization by increasing the number of seeds (in the range from Ne to 1.3 Ne), calculating all DVHs and finding the best solution, based on the reference DVH.
Results
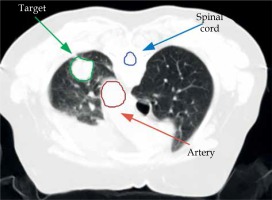
Lung adenocarcinoma case to test the method
Left lung adenocarcinoma case (Figure 6) with 21.22 cm3 of PTV was involved in this test. The spinal cord was chosen as OAR, and the type of seed was 6711 125I with strength of 0.7 mCi. The prescription dose for the tumor was 120 Gy. For OAR, the tolerate doses of the thoracic spine was 45 Gy [32]. In addition, it can be seen that the clinical data of lung at D2cc < 85 Gy had a lower risk in complication, so it was considered as the low-risk limits [33]. The total number of the voxels in the series of DICOM images and the extracted region for this case were 499 × 499 × 80 and 99 × 99 × 40, respectively. 16 non-coplanar needles were initially assigned, and the optimization algorithm took 9.8 seconds, with 24 seeds and 13 needles. Particularly, the non-coplanar needles were assigned based on the experience of the physician, taking about 10 minutes. In order to accurately assign the initial needles, the minimum distance between two needles of 10 mm and the organs at risk avoidance should be considered. The initial needles should be assigned to cover the target. Therefore, the number of initial needles can be determined. Figure 7 shows the DVHs curves obtained from the optimization of the seeds’ distribution for different number of seeds. In addition, Table 1 and Table 2 shows the important parameters of the corresponding DVH curves. As can be seen from the graph, the curves with a small seed number were below the reference line. As the number of seeds increased, the DVH curve shifted upward. The curve (V100 < 90%, V150 < 50%, V200 < 25%) below the reference line demonstrated that some parts of the tumor did not receive enough dose. As for the top black line (V100 > 90%, V150 > 50%, V200 > 25%), most of the tumor received the prescription dose. The vast majority of the tumor received a sufficient dose; however, a large part was exposed to excessive amount of radiation. At this stage, increasing the number of seeds to allow more areas to receive sufficient doses would lead to more regional overdose, which should be avoided.
Table 1
Comparison of different number of seeds of the hybrid inverse optimization algorithm in PTV
Table 2
Comparison of different number of seeds of the hybrid inverse optimization algorithm in spinal cord
Fig. 7
Dose volume histogram (DVH) diagrams of the optimal distribution of 20 seeds to 25 seeds after optimization
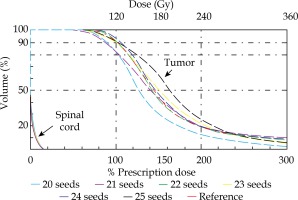
When the numbers of seeds are 22, 23, and 24, all the dose distribution generated by the inverse optimization algorithm can meet the clinical demand. In our study, through the DVH evaluation, 24 was chosen as the best seeds number. Clinically, on the premise of satisfying dose, the number of seeds should be as small as possible. Also, in order to reduce the injury of the puncture process and relieve the pain of the patient, the number of puncture needles should be the fewest possible as well, in view of meeting the dose requirements.
The coplanar puncture needles and non-coplanar puncture needles assigned to cover the target by physical therapists is presented in Figure 8. It was clear to see that the non-coplanar needle can easily avoid the bone to cover the target.
Fig. 8
A) The image on the left shows the best needle layout available under clinical conditions in the case of coplanar templates; B) The picture on the right shows the minimum number of needles used in the clinical use of non-coplanar needles
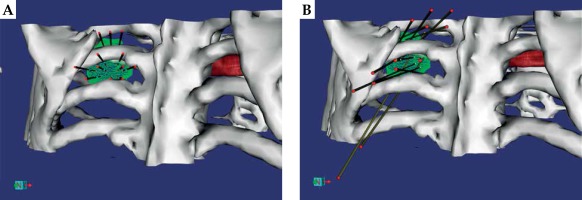
For coplanar template, 11 needles and 23 seeds were used to reach the best possible dose. However, the dose distribution did not reach the clinical requirement of terminating the tumor cells due to blocking rib. The dose parameters are described in Table 3.
Table 3
Dose parameters of PTV and OAR based on coplanar needles
| Name | Max dose(Gy) | Min dose(Gy) | Mean dose(Gy) | D90 (Gy) | V100 (%) | V150 (%) | V200 (%) | V10 (%) | V20 (%) | DHI | D2cc (Gy) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| PTV | 793 | 40 | 196 | 85 | 75.71 | 45.04 | 26.59 | – | – | 0.41 | 31 |
| OAR | 16.00 | 0 | 2.27 | 0 | 0 | 0 | 0 | 15.69 | 4.12 | – | – |
[i] D90 – minimum dose covering 90% of the target volume, V100 – target volume treated by the prescription dose, V150 – target volume treated by 150% of prescription dose, V200 – target volume treated by 200% of prescription dose, V10 – target volume treated by 10% of prescription dose, V20 – target volume treated by 20% of prescription dose, DHI – dose homogeneity index, PTV – planning target volume, OAR – organs at risk
Malignant tumor of spine case to test the technique
The tumor was 94.67 cm3 of PTV, and 63 seeds and 22 needles were used in the actual procedure. The simulation experiment was conducted under the same conditions as the surgery. The spinal cord was selected as organ at risk, and type 6711 125I seeds with strength of 0.5 mCi were used. The prescription dose for the tumor was 120 Gy. The total number of the voxels in series of DICOM images and the extracted region for this case were 499 × 499 × 170 and 99 × 99 × 90, respectively. According to nomogram, it was estimated that the number of seeds was 58, while the optimal result of the algorithm was actually 65 seeds. In addition, the procedure started with 30 needles but finally, 22 non-coplanar needles were used. The optimization algorithm took 20.5 seconds to obtain the ultimate optimal result.
As shown in Figure 9A, the tumor invaded the spinal cord, so the needle arrangement needed to avoid injuries to the spinal cord. The distribution of the non-coplanar needles is presented in Figure 9B, with spacing between 5 and 10 mm. Furthermore, it should be ensured that the needles cover all areas of the tumor and avoid interference. Figure 9C and Figure 9D are the dose coverage visualization of PTV by isodose curves and surfaces, from which we can directly screen the dose cold and hot points in the target area. As can be seen, the dose was able to meet the clinical requirements. In order to realize the clinical implementation of the new dose planning method, a three-dimensional template was designed to guide and hold non-coplanar needles as depicted in Figure 9E and Figure 9F.
Fig. 9
A) Reconstruction of target and spinal cord; B) 3D arrangement of the needles; C) 2D isodose curves display; D) 3D isodose surfaces display; E) Non-coplanar needle template model generation; F) 3D printing non-coplanar needles template
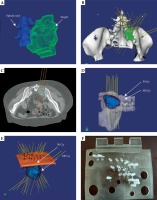
The dose parameters for the best optimal results are shown in Figure 10 and Table 4, in which the clinical dose requirements for PTV was met: V100 = 92.24 (V100 > 90%), V150 = 45.09% (V150 < 50%), and V200 = 14.63% (V200 < 25%). It should be noted that the tumor has greatly eroded the spine and the maximum dose to the spinal cord was 96 Gy. While in the case of high local dose, D90 = 1.3 Gy, V100 = 2.48%, and V200 = 2.06% were acceptable for clinical treatment.
Table 4
Dose parameters of PTV and spinal cord based on non-coplanar needles
| Name | Volume(cm3) | Max dose (Gy) | Min dose (Gy) | Meandose (Gy) | D90 (Gy) | V100 (%) | V150 (%) | V200 (%) | V10 (%) | V20 (%) | DHI | D2cc (Gy) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PTV | 94.67 | 807 | 80 | 192 | 121 | 92.24 | 45.09 | 14.63 | – | – | 0.88 | 50 |
| SC | 18.43 | 96 | 0 | 20 | 1.26 | 2.48 | 2.06 | 0 | 79.81 | 68.23 | – | – |
[i] D90 – minimum dose covering 90% of the target volume, V100 – target volume treated by the prescription dose, V150 – target volume treated by 150% of prescription dose, V200 – target volume treated by 200% of prescription dose, V10 – target volume treated by 10% of prescription dose, V20 – target volume treated by 20% of prescription dose, DHI – dose homogeneity index, PTV – planning target volume, SC – spinal-cord
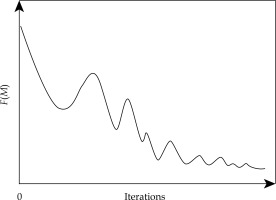
In the optimization, the progress of the objective function value against the number of iterations is presented in Figure 11. The curve was smoothed to show the trend of F(M) more clearly. The result demonstrated that there was a local minima in the optimization process, and the algorithm can escape from the local minima and converge to the global minimum.
Comparison with other algorithms
To better evaluate the proposed method in this research, we compared the result of malignant tumor of spine case with existing algorithms [14,34,35,36,37]. Most of the current inverse optimization algorithms were developed for prostate cancer. D’Souza et al. used a mixed-integer linear programming and a branch-and-bound algorithm to generate treatment plans [14]. An inverse optimization planning process utilizing a biologically-based objective was proposed [34]. The IPSA inverse planning algorithm was modified to include multiple dose matrices for the calculation of dose from different sources, and a selection algorithm was implemented to allow for the swapping of source type at any given source position [35]. The mixed integer programming was used to propose a volume-based objective function for dose optimization, which allowed for minimization of the number of under- or overdosed voxels in selected structures [36]. McGeachy et al. [37] used a simple genetic algorithm for dose optimization. The comparison results are shown in Table 5, including V100, V150, and the optimization time of each optimization algorithm [37].
Table 5
Comparison with existing inverse optimization algorithms
| Algorithm | V100 | V150 | Time |
|---|---|---|---|
| Radiobiology-based [34] | 90% | 70% | – |
| IPSA [35] | 95% | 73% | 106 s |
| Volume-based [36] | 92% | – | 20 min |
| Simple genetic algorithm [37] | 98% | 68% | 10 min |
| Deterministic search algorithm [14] | 96% | 50% | 20-45 min |
| Current research | 92% | 45% | 20.5 s |
In addition, we made a comparison using different size of single seed model to test the calculation speed and accuracy. As such, single seed models of 20 × 20 × 20 mm3, 40 × 40 × 40 mm3, and 50 × 50 × 50 mm3 were involved. The results show that it takes 2-4 seconds for 20 × 20 × 20 mm3, 6-9 seconds for 40 × 40 × 40 mm3, and 25-32 seconds for 50 × 50 × 50 mm3 in the optimization procedure. With reference to that, it also shows, the error is larger with smaller calculation range. The calculation error is more than 8% for 20 × 20 × 20 mm3, more than 5% for 40 × 40 × 40 mm3, and less than 5% for 50 × 50 × 50 mm3.
Discussion
In this paper, a hybrid inverse optimization method based on non-coplanar needles for CT-guided brachytherapy was proposed. The planning tool developed is capable of avoiding bones, decreasing needles and seeds, and automatically obtaining an optimal seed distribution.
From the result of the first case, it can be found that the non-coplanar needle and the hybrid inverse optimization method performed appropriately on the dose distribution in thoracoabdominal tumor. The non-coplanar needle has great advantages over coplanar, for that it can puncture at any angle, which helps to cover the whole target. In addition, as shown in Figure 8, non-coplanar needles can decrease the injury of normal tissues and avoid bones. As shown in Figure 8A, the coplanar needles were blocked by ribs, which increased the difficulty to reach satisfactory dosage. In contrast, as shown in Figure 8B, the non-coplanar needles were able to avoid the ribs and organs at risk. Additionally, the non-coplanar needles could reach almost any places in the chest and obtain a perfect dose distribution, something that coplanar needle could not achieve.
The application of the algorithm was verified through the second case, in which the treatment used 63 seeds and 22 needles, and the optimized results were 65 seeds and 22 needles. The inverse optimization algorithm was able to handle large tumors in real time for only 20.5 seconds and achieved a clinically accepted plan with 94.67 cm3 PTV. In terms of running speed, the hybrid inverse optimization method was fast enough to meet real-time dose planning requirements.
The advantages of using non-coplanar needle in the treatment planning have been discussed; however, assigning the non-coplanar needles’ position remains to be a challenge for a physician. Given that, the seed candidate position is attached to non-coplanar needles; the greater the number of needles is, the more time is required to find the optimal seed position (but better dose distribution would be obtained). Clinically, the recommended needles’ spacing is between 5 mm and 10 mm, while an excess of needles will be excluded by the hybrid inverse optimization method. Also, the needles in the same plane should be kept parallel as much as possible to prevent interference. Hence, a physician could combine the characteristics of non-coplanar needles mentioned before with clinical target coverage to improve the speed of the non-coplanar needle arrangement.
The hybrid inverse optimization method performs well in calculating the optimal seed distribution. It is based on the location of candidate seeds, which are indeed determined by the needle. However, from the running time of the two experiments, we can see that different tumor volumes need different optimization time and the larger tumor volume, the more time consuming. Owing to that, a larger target requires a greater number of needles, which produce a bigger number of seed positions candidate; the hybrid inverse optimization method would be more time consuming to find each quantity of seeds’ optimal results. We found that the speed of the hybrid inverse optimization method can be visibly improved by imputing initial geometric distribution. Through many simulation experiments, we found that the optimal seeds distribution always satisfied a rule. The seeds were densely distributed around the tumor, while the seeds distribution inside the tumor was sparse, and the distance between the seeds was at least 10 mm. Therefore, for larger targets, the initiation of seeds distribution according to this rule would greatly reduce the optimization time. In addition, a reasonable arrangement of non-coplanar needles to avoid too much dense arrangement would also contribute to time saving.
In the prostate brachytherapy, the recommended values by AAPM are V100 > 95% and V150 < 50%. In lung cancer brachytherapy, our hospital recommends V100 > 90% and V150 < 50%. From Table 5, we can see that the algorithms 1 and 3 did not meet the requirement of V100 > 95%. The other three algorithms 2, 4, and 5 met the requirement of V100 > 95%, but their V150 was more than 50%. The algorithm proposed in the current research met all the requirements of V100 > 90% and V150 < 50%. In terms of optimization time, the current research took less time (20.5 seconds) than other algorithms. Certainly, the improvement of the optimization result in target coverage and the optimization time will be the subject of future research. In addition to that, we have already finished the work of implementing the non-coplanar needles in clinical treatment. We managed to design a virtual template based on the extraction of a part of skin surface and print it on a 3D printer (Stratasys Object30pro).
As it is mentioned before, the 50 × 50 × 50 mm3 single seed model was used for optimization. But in the final dose and DVH computations, the 40 × 40 × 40 mm3 single seed model was used. According to the results, the calculation speed is faster when the single seed model is smaller, but the error is larger. When the dose calculation range is larger than 50 × 50 × 50 mm3, the calculation error will be much smaller, but the calculation time takes 2-4 or more minutes. We also compared the results of the dose calculation with the commercial TPS, such as VariSeed™ (Varian), Panther TPS (Prowess). The results demonstrated that the dose calculation using the 40 × 40 × 40 mm3 single seed model was consistent with the commercial TPS. The dose calculation error using the 50 × 50 × 50 mm3 single seed model was less than 5%. Therefore, to improve the optimization accuracy, we used the 50 × 50 × 50 mm3 single seed model.
Unquestionably, there was a limitation in this algorithm. The dose calculation formula was defined based on TG43 line source (2D) formalism, in which all seeds were assumed to be a part of the needle with proper orientations. However, in clinical surgery, the initial seeds orientations are usually unknown, which would result in an error in the actual dose distribution and the optimized results. Nevertheless, currently, there is no reasonable method to solve this problem, and in a future research, this issue will be thoroughly investigated. In addition, this study is a preliminary attempt in the optimization of non-coplanar needles, and no Monte Carlo or other advanced dose calculation methods were applied. In future, we will incorporate advanced algorithms, such as Monte Carlo to our proposed method. Furthermore, we hope to establish a technique to evaluate whether the distribution of the initial needle is reasonable. Because the initial needle is assigned by the physician according to clinical experience, a better seed distribution may be required. We also plan to incorporate a homogeneity index into the optimization algorithm to effectively avoid hot and cold spots, and to improve the optimization speed.
Conclusions
A hybrid inverse optimization method based on non-coplanar needles for CT-guided brachytherapy was proposed. The tool was able to arrange the non-coplanar needles to cover the tumor and avoiding organs at risk. In addition, the hybrid inverse optimization method has achieved a clinically acceptable dose distributions, which was effective for local tumor control. The hybrid inverse optimization last for 20.5 seconds in the tumor’s volume of 94.67 cm3, which is fast enough to be applied in practice.
We will continue our work on optimizing the hybrid inverse optimization method, which will be appropriate for multiple organs. We want to apply our method to intra-operation’s optimization by the detection of the real puncture needles and run the optimization based on the detected needles.